Mathematical Analysis of Flood-It Game
June 13, 2023
By Abhishek Pokharel
Supervisor: Professor David Seppala-Holtzman, PhD
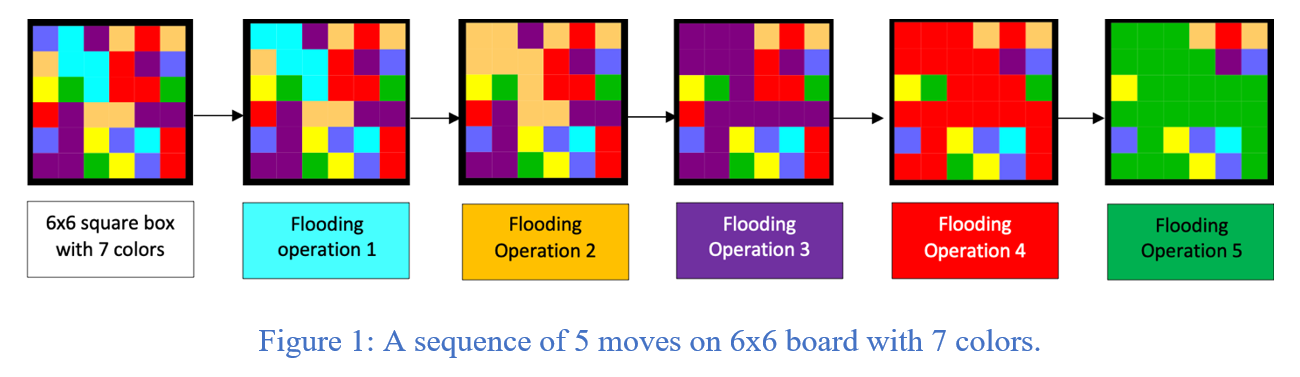
Flood-It is an engaging single-player online game that challenges players to fill an nxn board with a single color. The game board consists of square boxes, each initially filled with a different color. The player's objective is to use a limited number of moves, determined by the size of the board, to transform the entire nxn board into a uniform color.
In Flood-It, two or more square boxes are considered connected if they share the same color and are adjacent to each other. The game begins with the player initiating the flooding process from the top left corner square box. The player selects a color, which then spreads throughout the connected monochromatic region, changing the color of all the square boxes within that region. The flooding process continues as the player fills the region with the newly chosen color.
As the monochromatic region expands, the adjacent square boxes with the selected color become connected, gradually encompassing a larger portion of the nxn board. By strategically choosing colors and efficiently expanding the connected regions, the player aims to achieve the goal of filling the entire nxn board with the same color.
Figure 1 illustrates the initial moves of the Flood-It game, showcasing the gameplay for a 6x6 board with 7 different colors available.
In the Flood-It game, the player is challenged to achieve color uniformity on the game board within a specified number of moves, known as the target. The target value, denoted as 't', varies depending on the size of the board ('n') and the number of available colors ('c').
For example, when playing on a 10x10 board with 5 colors, the target is 14 moves. However, if the same 10x10 board has 8 colors, the target increases to 23 moves. Furthermore, the target value can differ even when the number of colors remains the same but the board size changes. For instance, on an 18x18 board with 5 colors, the target becomes 26 moves, unlike the 10x10 board with 5 colors.
The objective of this research is to determine the underlying function that precisely calculates the target value based on the given board size ('n') and number of colors ('c') on the game's website.
Lake and Island approach
The Lake and Island approach was initially employed to analyze the relationship between the perimeter of the partial lake (non-monochromatic regions) and the enclosed area. We conceptualized the nxn square box as a lake, with non-monochromatic regions representing islands.
To investigate this relationship, we examined individual tiny square boxes on the nxn board. Each tiny square box has a perimeter of 4 and an area of 1. As we progressed, we gradually added additional square boxes, considering both linear and non-linear shapes. We explored various conjectures, including the relationship between the perimeter (P), area (A), and shared edges (S).
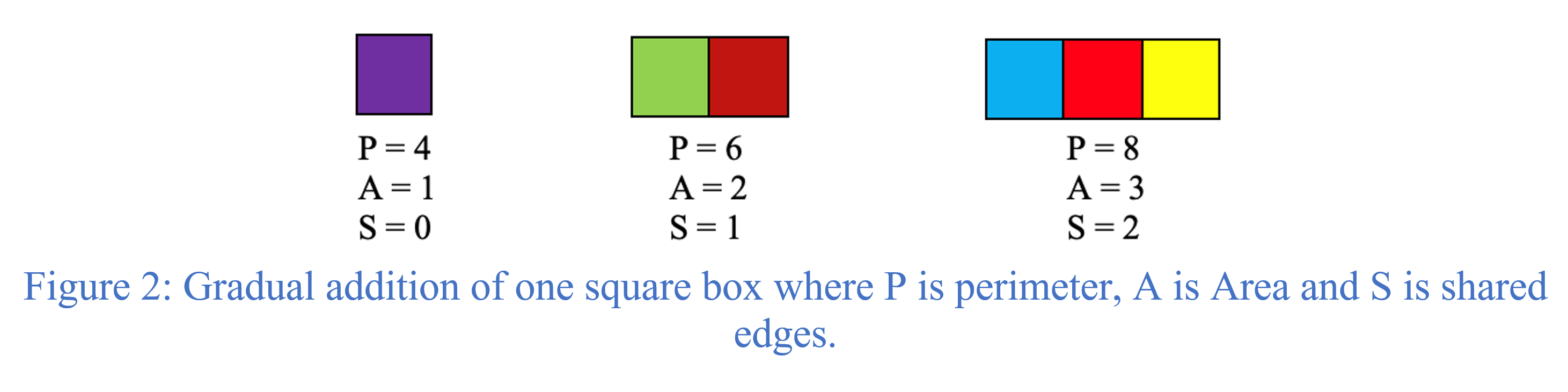
However, these conjectures failed to provide an exact perimeter for the conditioned nxn square box when we considered additional parameters such as usable perimeter, total perimeter, island area, and the number of colors. For instance, a conjecture 4A – 2S = P made form
(Figure 2) failed once we considered the usable perimeter, total perimeter, area of island and number of colors. Consequently, we determined the range of the perimeter by establishing a maximum and minimum value.
For the maximum perimeter, we proposed the formula 2A + 2 = P, as it accounted for the most linear cases. For the minimum perimeter, we suggested the formula Total Area = 4√A, based on the idea that a square is the most compact shape. By using these formulas, we derived the possible range of the perimeter.
To further explore this concept, we developed multiple programs in MATLAB. These programs considered factors such as the smallest and largest perimeter (floored values), number of colors, average area of any color that could be added, and active perimeter. In the case of non-static programs, we introduced weighting factors such as S and T. The program for non-static looked like this:

Where, n is the size, c is the color, M is average area of any color that can be added, P is the active parameter, S and T are the weighting factors, floor is the round down and +1 is to round up. We tested different ‘i’ with S and T for different n and c to calculate the exact target. However, we were not able to observe the exact pattern that changes in S(i) and T(i) affect in the target. We rejected the Lake and Island approach and started a new one.
The three-dimension approach
In the three-dimensional approach, we adopted a different method by plotting points in a three-dimensional space
(Figure 3).
This approach aimed to analyze the relationship between the number of colors (X-axis), the size of the square board (Y-axis), and the corresponding target number (Z-axis).
To begin, we plotted the values of 'N' (size) against 'T' (target) for each color. These data points were connected to form lines. We then utilized the least squares method to obtain the best-fit lines for each color.
Using the least squares approach, we attempted to generate a plane that approximated the entire surface. This plane would provide an estimation of the relationship between the number of colors, the size of the board, and the target number.
Mathematically expressing the above statement with color 4 for size 10x10, 14x14, 18x18 and 22x22 of target 11, 16, 21, and 26 respectively. We followed the similar idea for c = 5 and c =6. Hence, we plotted:
A= (4, 10,11), (4,14,16), (4,18,21), and (4,22,26) => Red in Figure 4
B= (5,10,14), (5,14,20), (5,18,26), and (5,22,32) => Blue in Figure 4
C= (6,10,17), (6,14,25), (6,18,32) and (6,22,39) => Green in Figure 4
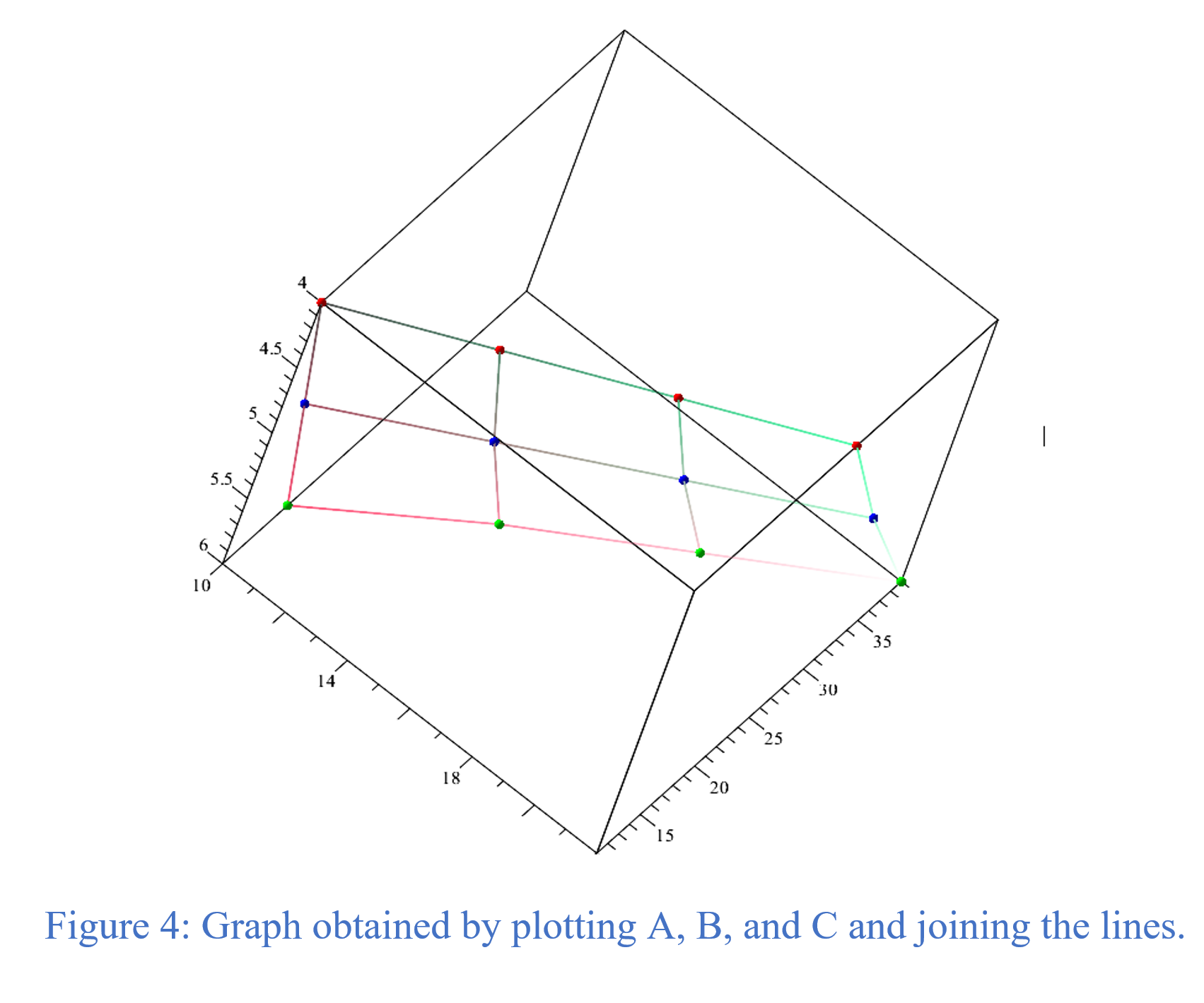
From these points we used the least square method to get best fit lines. In which we used n and t and the lines turned out to be almost perfect. Now, we took three points from which we generated two vectors whose cross product gave us a normal vector for our plane. Using three points P = (5,14,20), Q = (5,18,26) and R = (4, 14,16) we obtained an equation as follows:
We conjectured that this equation could be a good approximation for the function. By plugging in the data points into this equation, we obtained results that were close to, but not exactly equal to, the actual target values.
During our analysis, we noticed that when the number of colors ('c') increased while keeping the size ('n') fixed, the target also increased. Similarly, when the size of the board increased while maintaining a fixed number of colors, the target exhibited an upward trend.
To further investigate, we examined the relationship between the number of colors ('C') and the target ('T') using the least squares method. However, we observed that the resulting lines deviated more compared to the relationship between size ('N') and target ('T').
Consequently, we sought additional points of tangency to explore if they significantly differed from the plane formula we derived earlier (specifically for the case of (5,14,20)). We collected more data points, as it indicated the presence of curving points on the cylinder. These new data points allowed us to consider neighboring points for identifying points of tangency, enabling us to observe how they changed with higher values of 'c' and 'n'.
By incorporating additional data points into our analysis, we made a conjecture that for a fixed value of 'N', selecting the point of tangency as 'P = (C, N, T)' would allow the formula 'T = AC + BN + D' to accurately determine 'T' for any value of 'C'. We arrived at this conjecture by observing that different points of tangency resulted in different equations for 'T'.
Furthermore, we examined the cross product of vectors and determined the angles between their respective normal vectors. If these normal vectors were parallel, it would indicate a flat plane. However, since the normal vectors were not parallel, we utilized the angles to understand the degree of deviation and the direction in which they diverged.
These angle measurements provided valuable insights into the relationship between the normal vectors, allowing us to better understand how much they deviated and in which direction they trended. We know,
Following this concept, the dot product and the length between the normal vectors were calculated. From which the cosine angle was obtained.
Mathematically expressing the above statement. Let us consider P (5,10,14), Q (5,14, 20) and R (4,10,11) then normal vector was calculated which was N1 (-12, -6,4). Likewise, for A (5,14,20), B (5,18,26) and C (4,14,16) we obtained the normal vector N2 (-16, -6,4) and for X (6,18,32), Y (6,22,39), and Z (5,18,26) the normal vector was N3 (-24, -7, 4). Plotting N1, N2 and N3 we obtained Figure 5. Then the length of N1 was 14, N2 was 2√77 and finally the dot product of N1 and N2 was 244. The angle obtained was 6.741919759 degrees depicted in Figure 6.
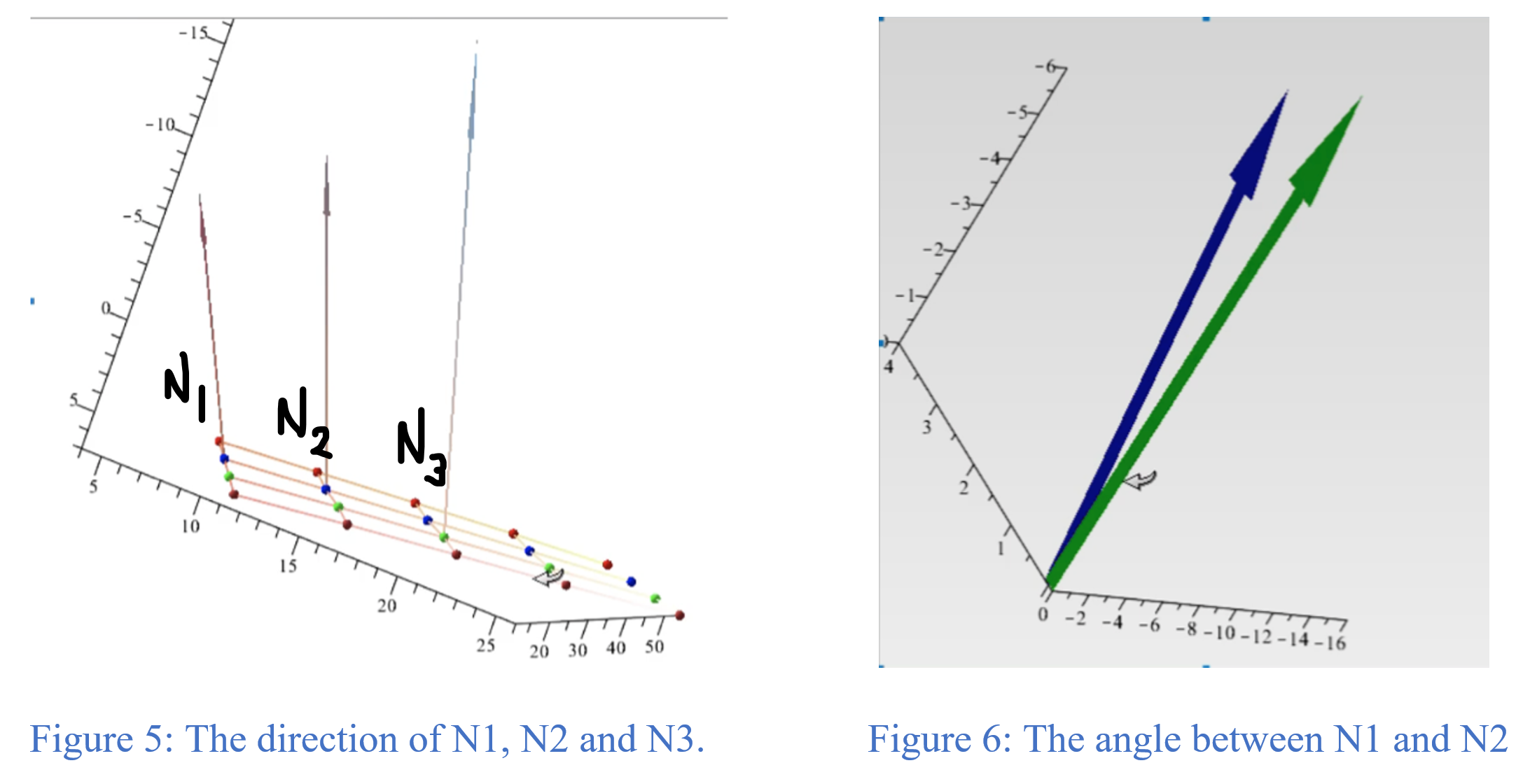
Similarly, the angle between different normal vectors were obtained in the same color and they varied with a small change. With the different color the angle changed drastically which was approximately similar through the different size in same color. The conjecture was in the same color ‘c’ and changing the size ‘n’ will change the with θdegree.
Conclusion
In summary, we were unable to discover the exact mathematical algorithm underlying how Flood-it operates. Nevertheless, we successfully identified the patterns that the game follows under different conditions. Through our analysis, we reached the conclusion that within a three-dimensional plane, selecting 'P = (C, N, T)' as the point of tangency allows the formula 'T = AC + BN + D' to accurately calculate 'T' for any given 'C'. Here, 'C' represents the number of colors used, 'N' denotes the size of the grid, and 'T' signifies the target. Additionally, we observed that the angle between the two normal vectors within the same color category remains relatively consistent, although the specific degree of the angle changes as the number of colors varies.